函数式编程：尾调优化

罗昭成 2024年08月09日

在函数式编程中， 函数是一等公民，实现中，会有很多代码都使用递归进行实现。在编写优雅代码的过程中，也会引入一定的风险：栈溢出。为了解决这个问题， 作为函数式编程风格的语言都会提供「尾调优化（Tail Call Optimization, TCO）」的特性。

什么是尾调用?

尾调用（Tail Call）指的是一个函数的最后一条语句是一个返回调用函数的语句，这个函数调用可以是对另一个函数的调用，也可以是对自身的调用。举个例子：

fun methodA(data:String): String {
  println("methodA Called")
  methodB(data)
  return methodC(data)
}

在上述代码中， methodB 与 methodC 都是函数调用，其中 methodC 是 methodA 返回前运行的最后代码，也就是所说的尾调用。如果最后这个调用函数是它自己，我们也称之为尾递归。

Kotlin中的尾递归优化

kotlin 是一种基于 JVM 的语言，它也支持函数式编程的思想。但是 JVM 因为其安全性限制，运行的程序无法操纵调用栈。基于常规的 JVM 方法调用，仅支持尾递归优化。

先来看一个简单的例子， 一个求和算法， 输入任一数字N，算出「1 ~ N」 所有数字的和：

fun sum(n: Int): Int {
    if (n == 1) {
        return n;
    } else {
        return n + sum(n - 1);
    }
}

代码使用递归的方式实现了求和算法，但是根据定义，这种写法是尾递归调用吗？当然不是。要将它改成尾递归调用，需要对代码进行调整， 示例代码如下：

fun sum(n: Int, result: Int): Int {
    if (n == 0) {
        return result;
    } else {
        return sum(n-1, n + result);
    }
}

此时进行测试调用，当 N = 10000 时，运行会出现如下错误：

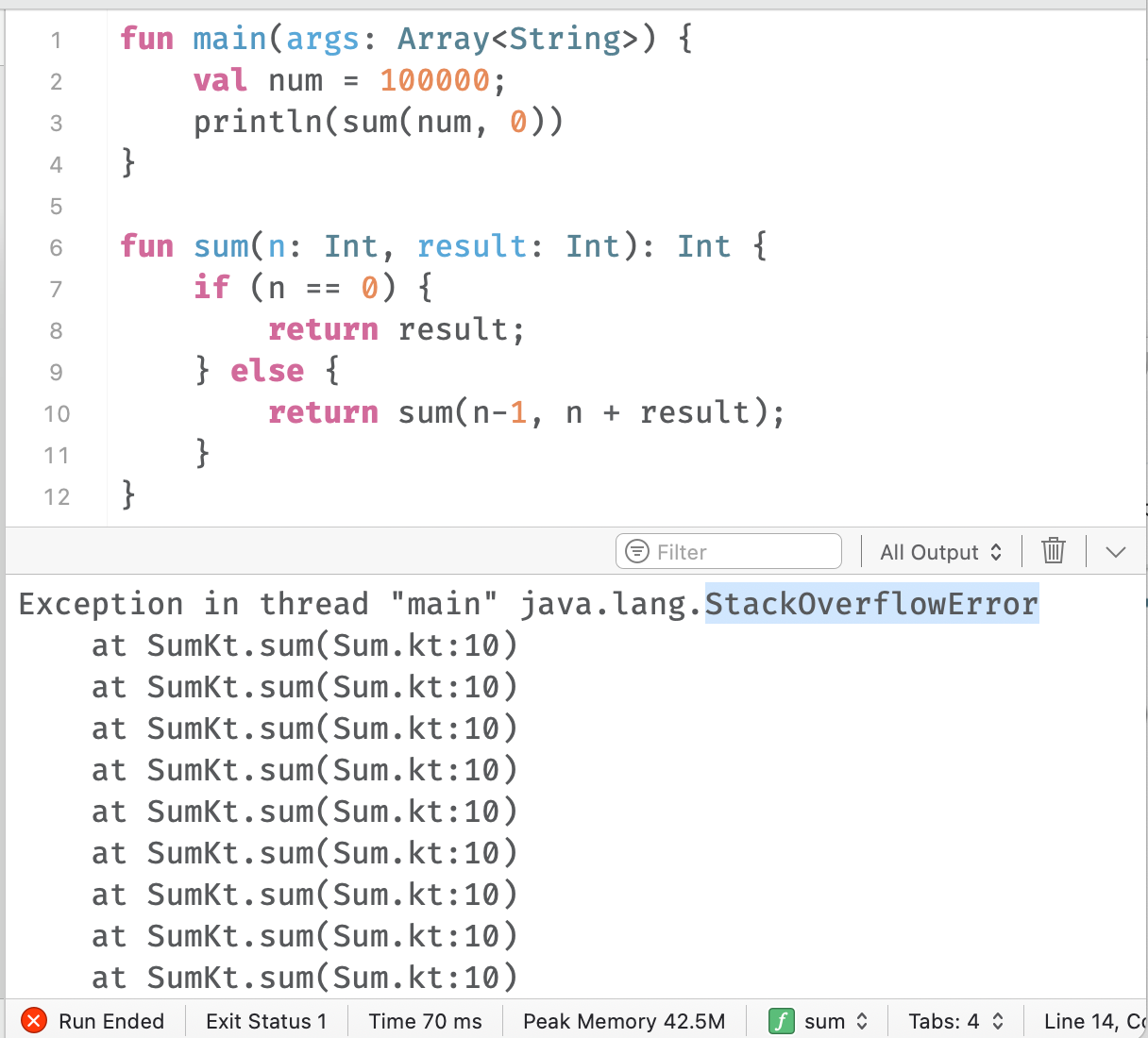
StackOverflowError

这个符合预期，出现了栈溢出。在 kotlin 中需要使用 tailrec 在申明当前方法为尾递归调用，需要进行优化，代码修改后运行结果如下：

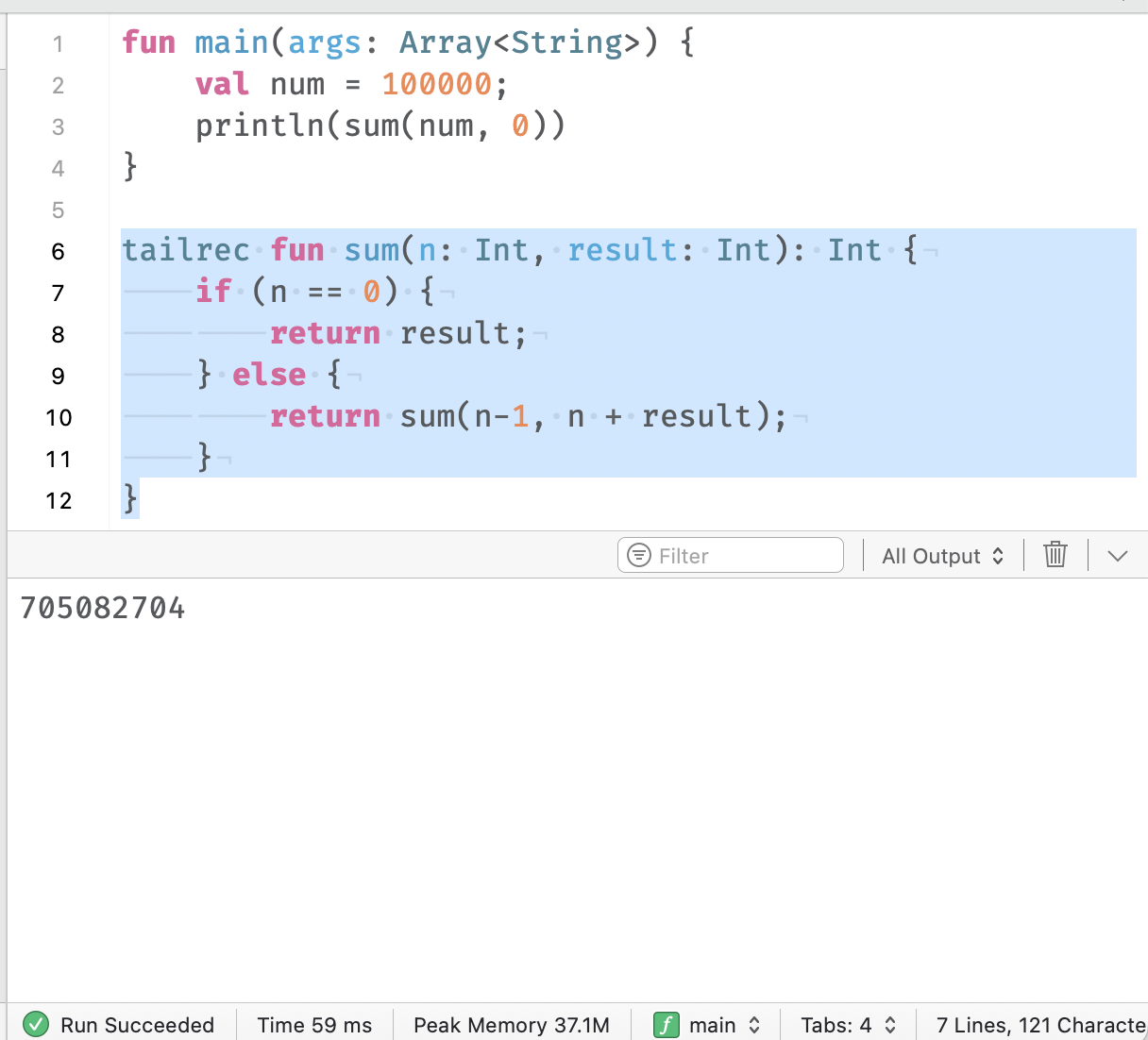
Run Success

问题来了，尾递归优化是如何实现的呢？

反编译编译后的 class 文件，可以看到，kotlin 在编译时，对代码进行了处理，将递归调用修改成了循环调用：

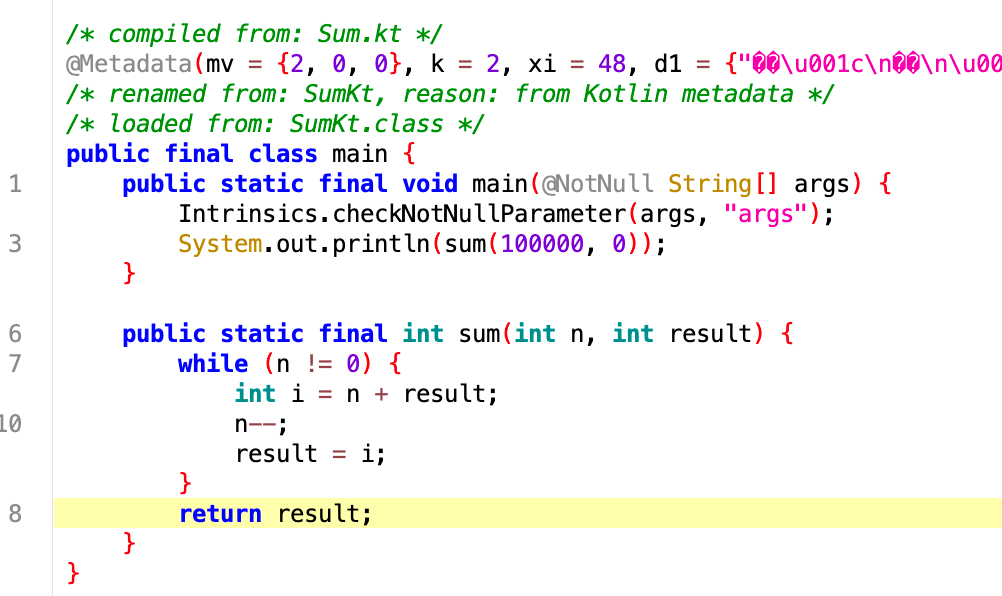
反编译后的结果

递归优化：Trampolining

对于上面的这个例子，要将他改成循环的形式也很简单，相信大多数开发都都能快速的完成，编译器也能很容易的完成上述转换。但在真实的开发场景中，要将一个复杂的递归改写成一个尾递归调用也不一定很容易，有没有简单的方法，可以将的递归算法都改写，以解决栈溢出的问题呢？

解决栈溢出的方法就是不用栈，而是将代码执行从递归栈修改为循环执行。在业界有一个叫做 Trampolines 的思想，就是用来实现转换的。它的核心思想是将递归调用转换为循环迭代，并在每次迭代中更新函数参数，而不是进行实际的递归调用。

还是上面所说的例子，求和：

fun sum(n: Int): Int {
    if (n == 1) {
        return n;
    } else {
        return n + sum(n - 1);
    }
}

使用 Trampolines 技术，先定义几个辅助类，代码如下：

sealed class Trampolines<out T> {
    abstract fun <U> flatMap(executor: (T) -> U): Trampolines<U>
    data class Done<out T>(
        val t: T
    ) : Trampolines<T>() {
        override fun <U> flatMap(executor: (T) -> U): Trampolines<U> {
            return Done(executor(t))
        }
    }

    data class Suspend<out T>(
        val suspension: () -> Trampolines<T>
    ) : Trampolines<T>() {
        override fun <U> flatMap(executor: (T) -> U): Trampolines<U> {
            return Suspend(fun(): Trampolines<U> {
                return this.suspension().flatMap(executor)
            })
        }
    }

    fun execute(): T {
        var temp = this
        while (true) {
            when (temp) {
                is Suspend -> {
                    temp = temp.suspension()
                }
                is Done -> {
                    return temp.t
                }
            }
        }
    }
}

求和算法也需要进行改写，代码改变后如下：

fun sum(num: Int): Trampolines<Int> {
    if (num == 0) {
        return Trampolines.Done(0)
    } else {
        return Trampolines.Suspend(fun(): Trampolines<Int> {
            return sum(num - 1).flatMap(fun(result: Int): Int {
                return result + num
            })
        })
    }
}

fun main() {
    println(sum(10000).execute())
}

看不懂？ 没关系，一行一行分析。 先来看一下 sum 这个方法，此时的写法与原来的递归写法差不多，完全符合函数式的风格。再来分析一下执行的逻辑：

  1. 传入的 num 为 0

此时拿到的是 Done 的对象，调用 execute 的时候，直接返回 0

  1. 传入的 num 大于 0 时，如 3

此时会直接返回一个 Suspend 对象， 并没有进行递归调用。调用 execute 方法时，才开始执行。此时再把视线移到 execute 方法里面，此时执行的是 temp.suspension() 的逻辑，即下面这个方法：

fun(): Trampolines<Int> {
    return sum(num - 1).flatMap(fun(result: Int): Int { return result + num})
}

这个方法干的第一件事是调用了 sum(num - 1) ，依然返回一个 Suspend 对象，在这个对象中存储了一个叫 suspension 的方法，紧接着调用 flatMap 方法又会返回一个新的 Suspend 对象，在这个 Suspend 对象中，可以访问到 suspension 方法。用这种对象链式的方法，将计算从递归转换成循环了，num = 3 的执行情况如下图：

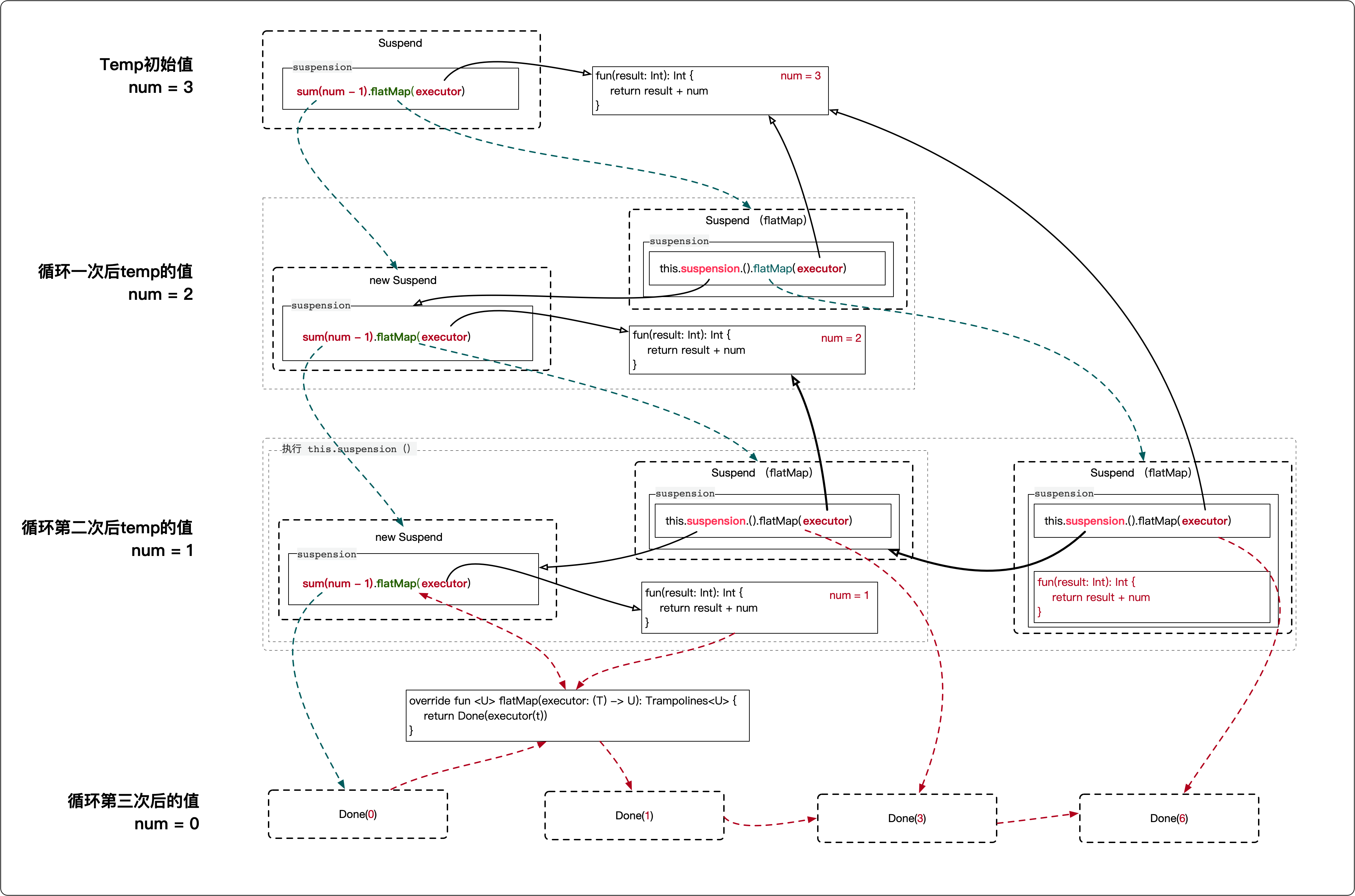
调用链路还原图

结语

文章中的内容介绍了递归以及解决递归栈溢出问题的模式，但这些内容仅仅是函数式编程思想中小小的一部分。

在代码 Copilot 发展如此迅速的时代，Bob 大叔依然为我们带来了他的新作：《函数式设计：原则、模式与实践》。在未来一段时间内，即使使用 GenAI 会让写代码的成本降低，但当出现错误时，其责任还是会落在开发者身上。学习函数式编程，有助于帮助我们：「保住已有的饭碗」、「寻找新的饭碗」、「保护自己的生命」。因此，不管在工作中是否有使用到函数式编程，都建议去学学。

Copyright © 2024 大罗说事